c00lHaX - Monkeys Typing Shakespeare
A Genetic Algorithm(GA) is a optimisation procedure inspired by natural selection. This belongs to the family of Evolutionary Algorithms. To put it very crudely, this class of algorithms attempts to maximize a fitness function (again, similar to it’s biological namesake) through a iterative procedure of selection, crossover and mutation.
Concretely, the algorithm can be defined as follows:
- Initialize a population to begin with. Every organism in the population will have a DNA. This DNA will be used to evaluate the fitness of the organism.
- The idea is to find the perfect organism (i.e. one that maximizes our fitness function). After initializing the population, we repeat following procedure till the max-iters are reached, or we find the perfect organism. The procedure is designed to birth better organisms through (1)selection, (2)crossover and (3)mutation.
- From the current population, select some organisms for DNA crossovers (or reproduction).
- Pick two organisms for the crossover and mix their DNA to return a new organism.
- Mutate the DNA of the new organism.
The Infinite Monkey Theorem
The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, such as the complete works of William Shakespeare.
Well, sure. It’s possible. This is no different than trying out every possible combination on a number lock – at some point you will arrive at the right sequence. But consider the likelihood of this actually happening.
Let’s assume our army of monkeys (cool band name?) were expected to produce Et tu, Brute?. To make things simple, we’ll limit ourselves to the lowercase alphabet and the space character and ignore everything else, leaving us with et tu brute. The probability of this particular sequence (assuming the typing is completely random) will be (1/27)^11 ~ 1.79e-16. That’s ridiculously small! We’ll need around 10 million BILLION tries to get this string by accident.
One way to improve our odds could be to understand how words are written – a character based langauge model for instance. This would limit the number of characters that could follow the first “e”. Another approach, could be to start from a randomly generated string and iteratively change characters so that we get closer to the target string : “et tu brute”. THIS is where we can use GA. By defining a fitness function which tells us how close are current organisms are to the target string, we can run the GA algorithm and generate it much faster.
Code
Organisms and Populations
An organism can be defined as follows:
class Organism:
def __init__(self, dna=None):
if dna is None:
self.dna = np.random.choice(vocab, target_len, replace=True)
else:
self.dna = dna
self.name = "".join(self.dna)
self.size = len(self.dna)
self.mid = self.size // 2
The initial DNA is a sequence of randomly chosen characters from our vocabulary (technically it should genes?).
At any point, we can evaluate the fitness of an organism by calling the fitness method.
def fitness(self):
return np.mean(self.dna == target_phrase)
Here, I simply calculate the fraction of characters which are in the right place; this is just one way to compute the fitness. If the fitness is 1.0, it means we’ve found the perfect organism. And yes, the target_phrase is a global variable. Sue me. To initialise the population, just create as many Organisms as you need.
Selection
Once the population is initialised, we create a pool of organisms for breeding. Again, there are many selection strategies. While you would definitely want to keep the organisms which have a stronger fitness value (survival of the fittest, only the strong survive…), but at the same time, maintain some diversity. A common approach is to sample organisms weighted by their fitness scores. This is the what I use.
def create_pool(org_list):
num = len(org_list)
scores = np.array([o.fitness() for o in org_list])
proba = scores / np.sum(scores)
return np.random.choice(org_list, num, p=proba)
Crossover
The organisms which survive the (natural)selection are then used for crossovers and producing new organisms with (hopefully)stronger DNAs. Again, there are many ways to crossover two DNA sequences. Here, I select two organisms at random, split drop the 2nd half of the first one and the 1st half of the second one, and then merge.
def crossover(a, b):
mid = a.mid
dna = np.hstack((a.dna[:mid], b.dna[mid:]))
return Organism(dna)
Mutation
This is done to explicitly maintain genetic diversity. For this problem, we randomly replace a gene in our DNA. In practice, we mutate rarely (here I set the mutation probability to 0.5%).
MUTATION_RATE = 0.005
def mutate(org):
new_dna = []
for gene in org.dna:
if np.random.rand() < MUTATION_RATE:
## mutate
new_dna.append(np.random.choice(vocab))
else:
new_dna.append(gene)
return Organism(np.array(new_dna))
And that’s it!
You keep repeating these three steps in a loop. After every iteration, check if you have found the perfect organism. Here’s what intermediate organisms look like when we try to generate the string “hello world” using our program.
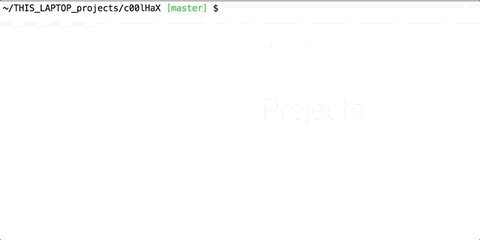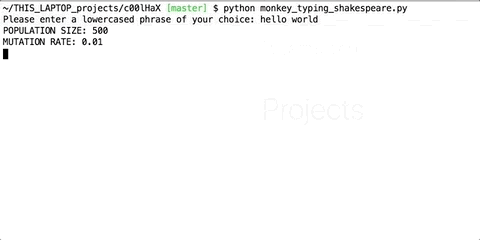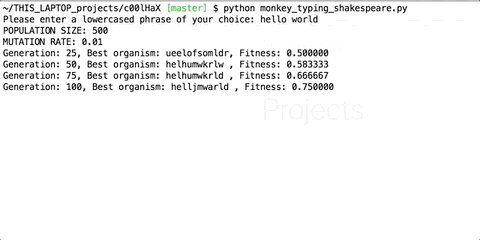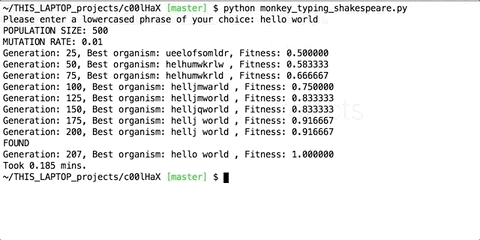
You can find the script to generate phrases here : https://github.com/priyamtejaswin/c00lHaX/blob/master/monkey_typing_shakespeare.py
Closing Thoughts
Recently, there’s been a fair amount of work done in this area by OpenAI and Uber. IIRC, Uber’s posts are actually what got me curious about this again. That, and this one video of a bot playing Mario which someone had shared in college. It was powered by this paper called “Evolving Neural Networks through Augmenting Topologies”. I’ll get down to reading the full paper and posting a review/summary soon. Till then, adieu!